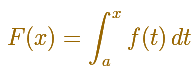
Si c pertecece a [a,b] y f es continua en c, entonces F es diferenciable en c, y
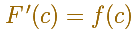
Una demostración visual bien conocida asume que la función f es continua en un entorno del punto (esta es una condición más débil, la hipótesis del teorema es más fuerte. Para una demostración analítica más rigurosa de este teorema hay que leer un buen libro de Cálculo).
Si c es un punto de (a,b), mirando la imagen podemos aceptar que
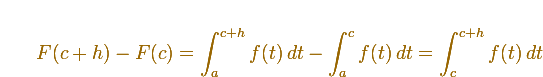
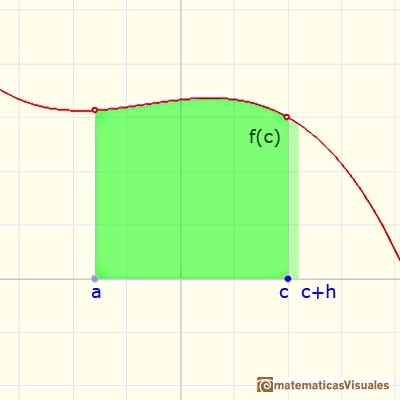
Si h es suficientemente pequeño (o podemos usar un teorema de valor intermedio, para ser más precisos)
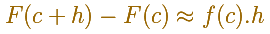
Dividiendo entre h:
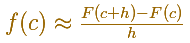
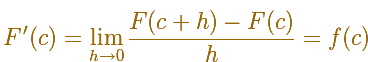
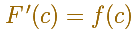
Si f tiene mejores propiedades, por ejemplo, si f es continua en todos los puntos de [a,b], entonces F es diferenciable en todos los puntos de (a,b) y
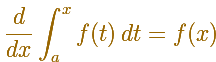
o
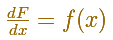
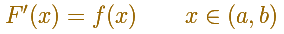
La idea es que empezamos con una función f:
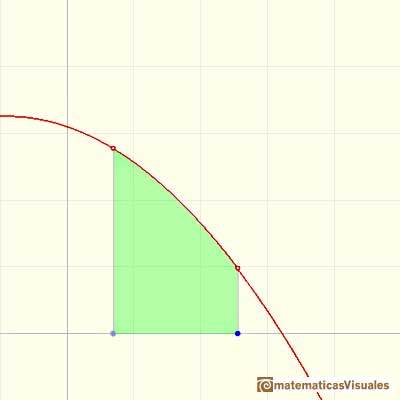
Consideramos una integral indefinida F (arrastando el límite inferior de integración obteneos diferentes funciones integrales):
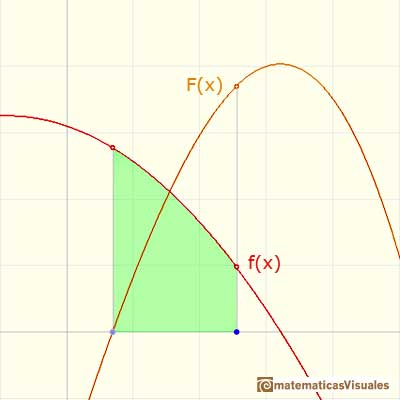
En un punto diferenciamos esta función F (gráficamente estamos considerando la pendiente de la recta tangente):
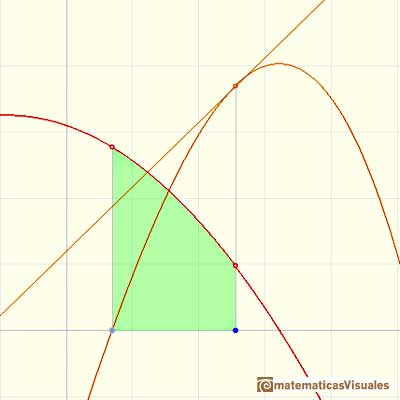
Entonces:
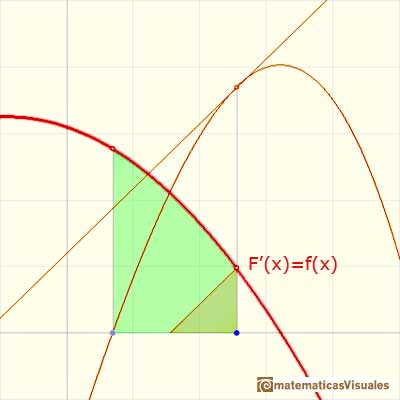
Este Teorema Fundamental del Cálculo nos dice que toda función continua tiene unaantiderivada y nos muestra cómo construir una usando una integral indefinida. Incluso funciones no diferenciables con esquinas, tales como el valor absoluto tienen una antiderivada.
Muchas veces el problema es cómo encontrar una antiderivada de una función, es decir, dada una función f(x), encontrar una función F(x) tal que F'(x) = f(x).
Un caso importante es cuando queremos integrar una función que tiene una antiderivada (o primitiva). Es decir, conocemos una función f y queremos integrar f' (o tenemos que integrar f' y podemos encontrar una primitiva f). En este caso, podemos ver la función que queremos integrar como una tasa de variación y la integral como un acumulador de este cambio (un ejemplo: la integral de la velocidad es la distancia recorrida).
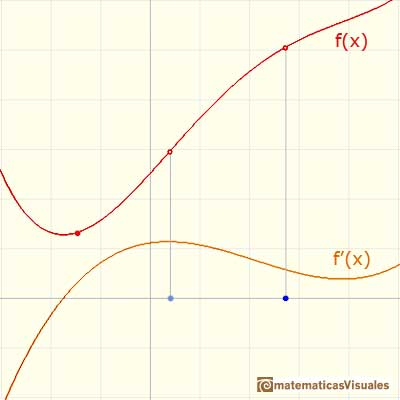
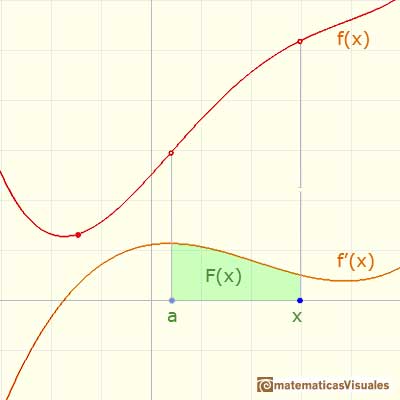
Definimos una función integral F (pero ahora estamos integrando f'):
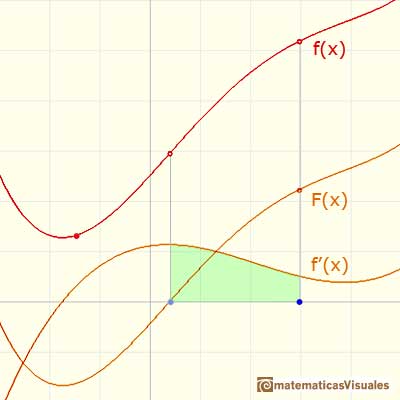
Entonces F es una primitiva de f', es decir:
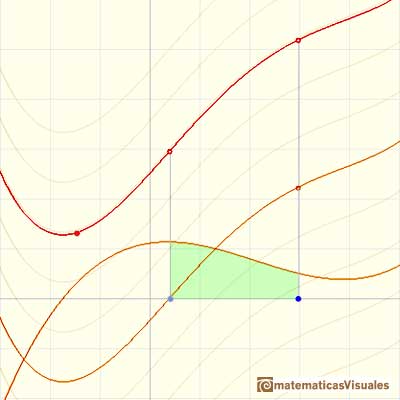
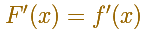
Podemos ver que
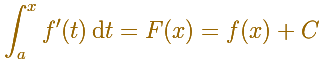
No hay comentarios.:
Publicar un comentario