La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
Notación
La notación que emplearemos para referirnos a una antiderivada es la siguiente:
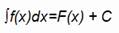
Teorema
Si dos funciones h y g son antiderivadas de una misma función f en un conjunto D de números reales, entonces esas dos funciones h y g solo difieren en una constante.
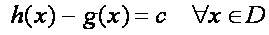
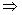
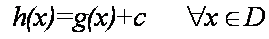
Conclusión: Si g(x) es una antiderivada de f en un conjunto D de números reales, entonces cualquier antiderivada de f es en ese conjunto D se puede escribir como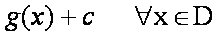 c constante real.
c constante real.
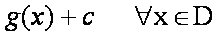 c constante real.
c constante real.
Fórmula que relaciona la integral definida y la indefinida
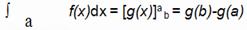 .
.
Para encontrar la antiderivada de cualquier función tenemos que contar con un formulario como el siguiente:

Estas son solo algunas de las fórmulas que existen. Vamos a utilizar la primera de ellas para resolver el siguiente ejemplo:
EJEMPLO 1
Ahora bien tenemos la siguiente función por resolver :
Para poder sacar la antiderivada tenemos que realizar lo que nuestra formula nos indica, n es el exponente de la X se le deberá sumar 1 todo eso quedara en el numerador y repetiremos esa suma de n+1 en el denominador.
Nos debe de quedar de la sig. manera:
Hacemos la suma tanto en denominador como en numerador y nos quedaría de la siguiente manera:
Se divide el número 2 que tenemos el numerador con el 2 que se obtuvo en el denominador:
Pero nunca debemos olvidar agregar en forma de suma una letra C de lo contrario estará mal, debemos hacerlo de la siguiente manera y así concluye:
EJEMPLO 2
Bien ahora vamos a sacar la antiderivada de la siguiente función

Para ello necesitamos la siguiente formula, esta nos dice que la integral de sen es - cos y esa parte es muy facil de comprender, pero ¿Qué es esa letra K en la formula?

Bueno como veras en el siguiente ejemplo " K " es la constante que multiplica la X de nuestra función
Bien ahora vamos a sacar la antiderivada de la siguiente función

Para ello necesitamos la siguiente formula, esta nos dice que la integral de sen es - cos y esa parte es muy facil de comprender, pero ¿Qué es esa letra K en la formula?
Bueno como veras en el siguiente ejemplo " K " es la constante que multiplica la X de nuestra función
Por lo tanto aplicando la formula obtendremos el siguiente resultado:


Considero que sería más correcto en el ultimo ejemplo, encerrar sen(kx), para no generar confusión.
ResponderBorrarMuy buen ejemplo
ResponderBorrarno esta bueno -.-
Borrarbuena explicación
ResponderBorrarno entendí el ultimo ejemplo, porque queda 4?
ResponderBorraro es el valor que le das a K?
Borrarestos ejemplos están excelentes, me ayudaron mucho.
ResponderBorrar