INTEGRAL x-n

Potencia de x.

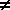xn dx = x(n+1) / (n+1) + C (n  -1)  Demostración

1/x dx dx = ln|x| + C

Exponente / Logaritmo

ex dx = ex + C  Demostración	bx dx = bx / ln(b) + C  Demostración
ln(x) dx = x ln(x) - x + C Demostración

Trigonométrica

sen x dx = -cos x + C  Demostración	cos x dx = sen x + C  Demostración	tan x dx = -ln|cos x| + C Demostración
csc x dx = - ln|csc x + cot x| + C	sec x dx = ln|sec x + tan x| + C	cot x dx = ln|sen x| + C

Resuelta Trigonométrica

cos x dx = sen x + C  Demostración	sen x dx = -cos x + C  Demostración	sec2 x dx = tan x + C  Demostración
csc x cot x dx = -csc x + C  Demostración	sec x tan x dx = sec x + C  Demostración	csc2 x dx = -cot x + C  Demostración

Trigonométrica Inversa

arcsen x dx = 1  (1-x2) + C	arccsc x dx = -1 |x|(x2-1) + C
arccos x dx = -1  (1-x2) + C	arcsec x dx = 1  |x|(x2-1) + C
arctan x dx = 1 1+x2 + C	arccot x dx = -1 1+x2 + C

Hyperbólica

senh x dx = cosh x + C	cosh x dx = senh x + C	tanh x dx = ln( cosh x ) + C
csch x dx = ln( tanh(x/2) ) + C	sech x dx = atan( senh x ) + C	coth(x) dx = ln( senh x ) + C