Es cualquier expresión del tipo: a1x1 + a2x2 + a3x3 + ... + anxn = b, donde ai, b 
 .
.

 .
.
ai son los coefecientes.
b es el término independiente.
xi son las incógnitas.
Solución de una ecuación lineal
Cualquier conjunto de n números reales que verifica la ecuación se denomina solución de la ecuación.
Ejemplo
Dada la ecuación x + y + z + t = 0, son soluciones de ella:
(1,−1,1,−1), (−2,−2,0, 4).
Ecuaciones equivalentes
Dos o más ecuaciones son equivalentes si tienen las mismas soluciones.
Sistemas de ecuaciones lineales
a11x1 + a12x2 + .....................+a1nxn = b1
a21x1 + a22x2 + .....................+a2nxn = b2
...............................................................
am1x1 + am2x2 + .....................+amnxn = bm
xi son las incógnitas, (i = 1, 2,...,n).
aij son los coeficientes, (i = 1, 2,..., m), (j = 1, 2,..., n).
bi son los términos independientes, (i = 1,2,...,m).
m, n 
 m > n, ó m = n, ó m < n.
m > n, ó m = n, ó m < n.

Obsérvese que el número de ecuaciones no tiene por qué ser igual al número de incógnitas.
Cuando n toma un valor bajo, es usual designar a las incógnitas con las letras x, y, z, t, ...
Cuando bi = 0 para todo i, el sistema se llama homogéneo.
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto deecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Solución de un sistema
Es cada conjunto de valores que verifica todas las ecuaciones.
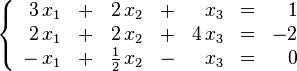
No hay comentarios.:
Publicar un comentario