DETERMINACION DE COSTOS

La determinación de costos es una parte importante para lograr el éxito en cualquier negocio. Con ella podemos conocer a tiempo si el precio al que vendemos lo que producimos nos permite lograr la obtención de beneficios, luego de cubrir todos los costos de funcionamiento de la empresa.

Los costos nos interesan cuando están relacionados directamente con la productividad de la empresa. Es decir, nos interesa particularmente el análisis de las relaciones entre los costos, los volúmenes de producción y las utilidades.

La determinación de costos permite conocer:

• Cuál es el costo unitario de un artículo, esto es, lo que cuesta producirlo


• Cuál es el precio a que debemos venderlo


• Cuáles son los costos totales en que incurre la empresa.


• cuál es el nivel de ventas necesario para que la empresa, aunque no tenga utilidades, tampoco tenga pérdidas. Es decir, cuál es el punto de equilibrio.


• Qué volumen de ventas se necesita para obtener una utilidad deseada.


• cómo se pueden disminuir los costos sin afectar la calidad del artículo que se produce.


• Cómo controlar los costos.

TIPO DE COSTOS

Al examinar los costos, se pueden separar en dos grandes rubros: COSTOS FIJOS Y COSTOS VARIABLES.

COSTOS FIJOS

Son periódicos. Se suele incurrir en ellos por el simple transcurrir del tiempo. Por ejemplo:

• Alquiler del local


• Salarios


• Gastos de mantenimiento


• Depreciaciones y amortizaciones

Cualquiera sea el volumen de producción que se pretenda lograr no se pueden evitar estos costos. Son independientes del nivel de producción.

COSTOS VARIABLES

Son los que están directamente involucrados con la producción y venta de los artículos, por lo que tienden a variar con el volumen de la producción. Por ejemplo:

• Las materias primas.


• Salarios a destajo o por servicios auxiliares en la producción


• Servicios auxiliares, tales como agua, energía eléctrica, lubricantes, refrigeración, combustible, etc.


• Comisiones sobre ventas.

La suma total de ambos con los COSTOS TOTALES

LOS COSTOS FIJOS

El siguiente ejemplo permitirá que nos demos cuenta de algunas características del comportamiento de los costos fijos.

Don Gustavo Fernández se ha decidido a establecer una pequeña fábrica de zapatos. Alquila un local, contrata trabajadores, compra máquinas, etc. Al cabo de un año de trabajo se percata de que el primer mes no produjo ningún artículo, pues a pesar de que tenía todo listo, aún no contaba con el permiso de fabricación de los zapatos cuya marca debía registrar. En febrero produjo 500 pares; en marzo 800, en abril 1000 y de mayo a diciembre produjo 1200 pares cada mes.

Con la información anterior, elaboró una gráfica para analizar el comportamiento de los costos del alquiler, los salarios, los servicios públicos, etc. Todos estos suman la cantidad de 6000 pesos mensuales. Obtuvo el siguiente resultado:

MES	Costo Fijo	Producción	Costo fijo por par
Enero	6000	0	6000
Febrero	6000	500	12
Marzo	6000	800	7.5
Abril	6000	1000	6
Mayo	6000	1200	5
Junio	6000	1200	5
Julio	6000	1200	5
Agosto	6000	1200	5
Septiembre	6000	1200	5
Octubre	6000	1200	5
Noviembre	6000	1200	5
Diciembre	6000	1200	5
TOTAL	72000	11900

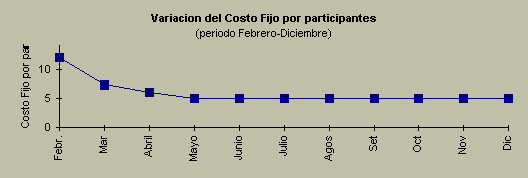
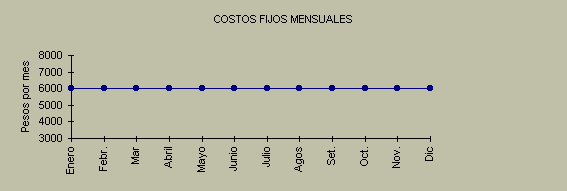
Como puede observarse, el importe total del costo fijo mensual no se modifica. Igual costó en el mes de enero en el que no se produjo nada, que los meses en los que se produjeron diversas cantidades: 500, 800, 1000 y 1200 pares respectivamente.

Esto nos indica por lo menos dos cosas:

• Los costos mínimos de la empresa están determinados principalmente por los costos fijos.


• Si son los mismos costos fijos se puede producir un mayor volumen de artículos, entonces los costos fijos de cada artículo producido serán menores, pues se prorratearán todos los costos en un mayor número de unidades.

 COSTOS VARIABLES

Don Gustavo Fernández debe adquirir un conjunto de materias primas para elaborar los zapatos. Cuero, tela, pegamento, solventes, agujas, etc. Toda esta materia prima llega a convertirse en parte del producto terminado. Por eso los costos de esos insumos, se cargan directamente a las unidades del producto, sin utilizar el prorrateo: es decir que cada unidad producida tendrá (debería tener) el mismo costo en lo que se refiere a materiales. Esto significa que si en un par de zapatos se invierten $ 10 en materia prima, 2 pares costarán $ 20 en materia prima, y 1000 pares costarán $ 10000 en materia prima, y así sucesivamente. En otras palabras: al crecer el volumen de los artículos que se producen crecen también los costos variables.

COSTOS TOTALES

Por definición, y como se mencionó anteriormente, los costos totales incurridos en la operación de una empresa durante un periodo dado, se cuantifican sumando sus costos fijos y variables, expresándose esta relación según se indica a continuación:

COSTOS TOTALES = COSTOS FIJOS + COSTOS VARIABLES

Así, en el ejemplo que nos ocupa, Don Gustavo hizo la siguiente gráfica, ilustrando el comportamiento de los costos fijos, variables y totales de la empresa durante el año de operación

Meses	Costos Fijos	C. Variables	Costos Totales
Enero	6	0	6
Febrero	6	5	11
Marzo	6	8	14
Abril	6	10	16
Mayo	6	12	18
Junio	6	12	18
Julio	6	12	18
Agosto	6	12	18
Setiembre	6	12	18
Octubre	6	12	18
Noviembre	6	12	18
Diciembre	6	12	18
			191 000

REDUCCION DE COSTOS

Algunas posibilidades de reducir los costos consisten en lo siguiente:

DE LOS COSTOS FIJOS

Los costos fijos se realizan para mantener una capacidad instalada de producción. Por ello las mejores formas de reducirlos pueden ser:

Aprovechar al máximo la capacidad instalada.

• Por producción masiva


• Por uso de técnicas diferentes.
• Por cambios administrativos.
• Por cambio de maquinarias y equipos.

Mejorar la productividad del personal

• Con una mejor comunicación


• Con incentivos que los estimulen.
• Con evaluaciones y controles periódicos.

DE LOS COSTOS VARIABLES

Se incurre en costos variables para adquirir la materia prima (y otros insumos) que se transformará. Por ello las formas de reducir los costos variables pueden ser:

Planear la producción masiva que permita realizar compras en volúmenes con los que se pueda obtener descuentos.

Investigar los precios de mercado en las materias primas y comprar al proveedor que ofrezca el costo más económico con la misma calidad.

Mejorar el rendimiento de las materias primas.

• Mediante el control de desperdicios y artículos defectuosos.


• Mediante diseños que optimicen el empleo de la materia prima.

COSTO UNITARIO

Si los costos totales de la empresa son igual a Costos Fijos más Variables, no es difícil suponer que el costo total unitario es igual a la suma del costo fijo unitario más el costo variable unitario.

COSTO TOTAL UNITARIO = COSTO FIJO UNITARIO + COSTO VARIABLE UNITARIO

Estimar el costo total unitario es muy importante, porque consiste en la cotización que se suele hacer para establecer el precio de venta del artículo que se produce. Generalmente se estiman antes de que se realice la producción y entrega de productos. Por eso se les conoce como costos estándar.

Los costos totales unitarios o estándar son los que deben efectuarse en condiciones normales de fabricación del producto. Tienen una importancia destacada en el proceso de planeación de la producción y en el proceso de control, ya que implican una conducta normativa y, señalan cuál debe ser el esfuerzo empleado para lograr lo que debiera ser como propósitos de producción de la empresa.

Los costos unitarios totales dependerán de:

1. El costo de las materias primas.


2. El rendimiento de las materias primas.


3. El costo de los salarios.


4. La eficiencia de la mano de obra.


5. Los beneficios de la especialización productiva.


6. El presupuesto de gastos.

La estimación del costo unitario permite al empresario elaborar presupuestos de operación de la empresa, así como establecer el programa tentativo de producción.

Conocer el costo total unitario me permite elaborar mi política de precios, sin arriesgarme a tener pérdidas

 Y nos indica lo que cuesta producir un artículo en nuestra empresa

 

CALCULO DEL COSTO UNITARIO

El cálculo del costo variable unitario se realiza como ya se especificó. Si es necesario conviene que lo revise antes de continuar. El costo fijo unitario se puede efectuar de varias formas.

Se puede tomar el total de los costos fijos realizados el mes anterior. Esta cantidad se divide entre el número de productos elaborados en el mismo mes o por la cantidad de productos que se estima se lograrán producir durante el mes que se programa.

Este es un cálculo del costo fijo unitario muy sencillo. Sin embargo, no es el único tipo de cálculo. Hay otras formas de calcularlo, que son empleadas por la cantidad de información que proporcionan y, las ayudas que proporcionan para el control del rendimiento de los trabajadoras.

Se puede calcular mediante la suma de todas las horas de trabajo empleadas. Por ejemplo, Don Gustavo tiene tres trabajadores empleados en el proceso de producción. Cada uno de ellos trabaja 40 horas a la semana, por lo que al mes cada uno trabaja aproximadamente 140 horas. En total los tres empleados trabajan 520 horas mensuales.

Los costos fijos de la empresa se dividen entre el total de horas trabajadas, con lo que se obtiene el costo fijo por hora trabajada.

Luego se calcula la cantidad de tiempo que se requiere para que se transformen las materias primas en el producto terminado. Por ejemplo, puede ser que para la fabricación de un participantes de zapatos se empleen dos horas.

Finalmente se multiplica el costo fijo por hora trabajada por la cantidad de horas necesarias para producir la unidad del artículo. El resultado es el Costo Fijo Unitario.

Como se puede apreciar en ambas formas de calcular el costo fijo unitario se efectúa un prorrateo; es decir, se reparte proporcionalmente la cantidad de los costos totales de la empresa entre los productos elaborados. Los costos se pueden prorratear cuando se producen unidades homogéneas (todas iguales). Si se producen unidades diferentes debe hacerse un cálculo para cada clase de producto.

Una vez que se tienen el costo fijo unitario y el costo variable unitario, se calcula el costo total unitario, sumando ambos. Luego se puede calcular la Utilidad Neta:

UTILIDAD NETA UNITARIA = PRECIO DE VENTA - COSTO TOTAL UNITARIO

El manejo de toda esta información, a través de la determinación de costos que usted implante en su microempresa, le permitirá establecer precios adecuados a sus productos. En la unidad de Ventas, tendrá información sobre cómo calcular los precios.

PUNTO DE EQUILIBRIO

Con tantos problemas económicos, ya no sé cuánto es lo mínimo que tengo que producir y vender para poder salir adelante

El punto de equilibrio de una empresa industrial, es aquel en el que a un determinado nivel de operación, ésta no obtiene utilidades, pero tampoco incurre en pérdidas.

Asimismo, este concepto presenta dos variantes: el Punto de Equilibrio Operativo (PEO), el cual se desarrolla a continuación, y el Punto de Equilibrio Financiero (PEF), el cual veremos más adelante.

En la práctica, el análisis del punto de equilibrio de una empresa, en función de la información disponible, se realiza considerando un periodo determinado, normalmente un año.

Previo al desarrollo de este aspecto en el ejemplo de la microempresa de Don Gustavo, es necesario tener presente los siguientes conceptos:

Ø Contribución Marginal por Unidad: entendida ésta como la diferencia entre el precio de venta de la unidad y los costos variables incurridos para producirla. Se expresa por la relación:

Contribución Marginal por Unidad = precio de venta unitario - costo variable unitario

Ø Punto de Equilibrio Operativo (PEO) en unidades físicas: representa la cantidad de unidades físicas que es necesario producir y vender, a fin de alcanzar el nivel de operación de la empresa sin utilidades ni pérdidas. Esta relación se expresa por:

Punto de Equilibrio Operativo (PEO) en unidades físicas = Costos fijos

Contribución marginal por unidad

Ø Punto de equilibrio operativo (PEO) en unidades monetarias: Resulta de multiplicar el punto de equilibrio operativo en unidades físicas por el precio de venta unitario. La expresión a considera es:

Punto de Equilibrio Operativo (PEO) en unidades monetarias: PEO unidades físicas x Precio de venta unitario

Su interpretación es similar a la del concepto anterior, considerando únicamente el cambio en la cantidad de unidades, de físicas (productos) a monetarias.

Una vez expuestos estos conceptos, a continuación procederemos al análisis del punto de equilibrio operativo (PEO) . Don Gustavo realiza las siguientes consideraciones:

• Se determina que cada participantes de zapatos se vende a $ 30


• Los costos variables por cada par son de $ 16.05 por unidad, resultado obtenido del cociente entre los costos variables totales y el número de unidades producidas en el período de un año; esto es:

$ 191.000 = $ 16.05 por par

11900 pares

• Según se indicó en su momento, independientemente del volumen de unidades producidas, para la operación de la empresa los costos fijos se mantienen en un nivel constante durante el periodo considerado.

Una vez precisadas las cifras de las consideraciones a emplear, en ese momento es posible determinar algebraicamente el PEO, tanto en unidades físicas como monetarias, para lo cual observaremos los siguientes pasos:

Determinación de la contribución marginal por unidad:

Contribución Marginal por Unidad = Precio de venta unitario - Costo variable unitario

Contribución Marginal por Unidad = $ 30 - $ 16.05 = $ 13.95 por unidad

Cálculo del punto de equilibrio operativo (PEO)

En unidades físicas:

PEO en unidades físicas = Costos fijos del periodo

Contribución marginal por unidad

PEO en unidades físicas = $ 72000 = 5162 unidades

$ 13.95

En unidades monetarias:

PEO en unidades monetarias = PEO en unidades físicas x Precio de venta unitario

PEO en unidades monetarias = 5162 unidades x $ 30 = $ 154860

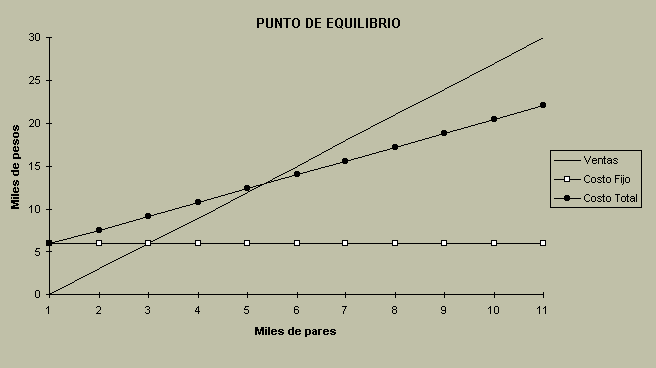
En términos generales, para elaborar la gráfica del punto de equilibrio operativo (PEO) se procede de la siguiente manera:

1. Calcúlelo de acuerdo al procedimiento visto anteriormente.


2. Dibuje a escala el eje horizontal de la gráfica. En él va a representar las unidades producidas y vendidas. Procure que la cantidad de unidades del punto de equilibrio quede en el centro del eje: luego distribuya intervalos iguales antes y después del punto central.


3. Dibuje a escala el eje vertical de la gráfica. En él va a representar la cantidad de dinero que se invierte en costos fijos y variables, y que se obtiene en concepto de ventas. Procure que la cantidad del volumen de ventas correspondiente al punto de equilibrio quede en el centro del eje. Luego distribuya hacia arriba y hacia abajo, en intervalos iguales, cantidades que representen diferentes volúmenes de producción y ventas.


4. Dibuje la recta que representa los costos fijos.


5. Trace una línea horizontal a partir del total de ventas en unidades monetarias, necesario para el punto de equilibrio.


6. Trace una línea vertical que vaya desde la cantidad de artículos del punto de equilibrio hasta la el punto de intersección con la línea horizontal anterior. Este punto representa el Punto de Equilibrio en las operaciones de la empresa.


7. Trace la línea de costos totales de la empresa. Recuerde que los costos totales son los costos fijos más los costos variables. Por eso debe trazarse la línea de costos totales desde el nivel de los costos fijos. Esta línea debe cruzar por el punto de equilibrio ya registrado en la gráfica y, prolongarse hasta el término de la misma.


8. Proyecte la línea de ventas. Esta se inicia en el nivel cero de unidades y cero de pesos, pasa por el punto de equilibrio ya registrado y se prolonga hasta el término de la gráfica.


9. Identifique cada línea y área.

Producción	Ventas	Costo Fijo	Costo Total
0	0	6000	6000
1000	30000	6000	7 605
2000	60000	6000	9 210
3000	9000	6000	10815
4000	12000	6000	12420
5000	15000	6000	14025
6000	18000	6000	15630
7000	21000	6000	17235
8000	24000	6000	18840
9000	27000	6000	20445
10000	30000	6000	22050

Advertisement

SINTESIS SOBRE COSTOS

Por costos se entiende el consumo de recursos, dinero, materiales y trabajo, que se capitalizan en los bienes que aumentan el valor con dichos consumos.

El devenir de los recursos en el ciclo económico de la empresa, compras, almacenamiento, transformación, transporte, ventas y cobranzas, son costos capitalizables. Es decir, son costos que se recuperarán en la fase final del ciclo económico: la de ventas y cobranza, así como también se obtendrá el beneficio correspondiente.

VALOR PRESENTE Y VALOR FUTURO

El valor del dinero en el tiempo es clave en Finanzas, en el sentido que siempre un peso hoy vale más que un peso mañana. Para efectos de calcular en forma homogénea los flujos que ocurren en distinto momento en el tiempo, debemos llevar todos estos a un valor presente [...]

Uno de los aspectos clave en finanzas es el del valor del dinero en el tiempo, en el sentido que siempre un peso hoy vale más que un peso mañana. Para efectos de poder calcular en forma homogénea los flujos que ocurren en distinto momento en el tiempo, debemos llevar todos estos a un valor presente o a un valor futuro, por lo que:

Foto: El Mercurio

Para el valor futuro o presente hay un tema clave: el valor del dinero.

Valor Presente: Es una manera de valorar activos y su cálculo consiste en descontar el flujo futuro a una tasa de rentabilidad ofrecida por alternativas de inversión comparables, por lo general denominada costo de capitalo tasa mínima.

Valor Futuro: Es la cantidad de dinero que alcanzará una inversión en alguna fecha futura al ganar intereses a alguna tasa compuesta.

El valor que en cualquier caso calculemos depende de los flujos de caja generados por el activo.  Es decir, depende de su tamaño, tiempo y riesgo. También, y muy críticamente, el valor depende del costo de oportunidad, ya que para realizar una valoración se deben tener los flujos que ocurren en distintas oportunidades en el tiempo, con riesgos distintos, en una base comparable.

A modo de ejemplo, si usted hoy deposita $1.000 en una cuenta que genera una tasa de interés de 10% anual, ¿cuánto tendrá usted al cabo del primer año?

Su valor futuro al final del primer año será de $1.100, que se calcula como $1.000 x (1+0,1) = $1.100

Si vuelve a depositar íntegramente la cantidad de $1.100 por un año más., ¿cuánto tendrá al concluir el año 2?

Durante ese año ganará 10% de interés sobre los $1.100. Así, el interés ganado será 0,10 x $1.100, o sea $110. Tendrá, pues, $1.210 al final del año 2 = $1.000 x 1,1 x 1,1 = $1.000 x 1,12= $1.210

Para entender la naturaleza del concepto del interés compuesto, podemos dividir el valor futuro de $1.210 obtenido en el ejemplo anterior, en 3 componentes:

a) Capital original de $1.000

b) Interés Simple: Es el interés sobre el capital original, $100 en el primer año y otros $100 en el segundo año ($200 en el ejemplo).

c) Interés Compuesto: Es el interés ganado sobre un interés ya obtenido, existen $10 de intereses ganados en el segundo año sobre los $100 de los intereses ganados en el primer año.

En el ejemplo, el Interés Total ganado ($210) es la suma del Interés Simple ($200) más el Interés Compuesto ($10).

En general se tiene que:

Foto: El Mercurio

Valor Futuro es la cantidad de dinero que alcanzará una inversión en alguna fecha futura.

Valor Futuro (VF) = Valor Presente x (1+r)t , o:

Donde:

• Valor Futuro es el flujo de caja a recibir o dar en un momento determinado en el futuro
• r es la tasa de interés en un período de un instrumento de riesgo comparable
• t es la cantidad de períodos que existe hasta un momento determinado en el futuro

Todos los valores presentes están medidos en $ de hoy.  Si tenemos $100 hoy más otros $60 hoy, en total tengo $160.  Es decir, los valores presentes son aditivos.

En artículos futuros seguiremos explicando estos conceptos que son de gran utilidad a la vez que necesarios cuando se analiza el valor del dinero en el tiempo.

DETERMINANTE

En Matemáticas se define el determinante como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.

Los determinantes fueron introducidos en Occidente a partir del siglo XVI, esto es, antes que las matrices, que no aparecieron hasta el siglo XIX. Conviene recordar que los chinos (Hui, Liu. iuzhang Suanshu o Los nueve capítulos del arte matemático.) fueron los primeros en utilizar la tabla de ceros y en aplicar un algoritmo que, desde el Siglo XIX, se conoce con el nombre de Eliminación de Gauss-Jordan.

La historia de los determinantes

Los determinantes hicieron su aparición en las matemáticas más de un siglo antes que las matrices. El término matriz fue creado por James Joseph Sylvester, tratando de dar a entender que era “la madre de los determinantes”.

Algunos de los más grandes matemáticos de los siglos XVIII y XIX contribuyeron al desarrollo de las propiedades de los determinantes. La mayoría de los historiadores coinciden en afirmar que la teoría de los determinantes se originó con el matemático alemán Gottfried Wilhelm Leibniz (1646-1716) quien fue con Newton, el co inventor del cálculo diferencial e integral. Leibniz empleó los determinantes en 1693 con relación a los sistemas de ecuaciones lineales simultáneas. No obstante hay quienes creen que el matemático japonés Seki Kowa hizo lo mismo unos 10 años antes.

Las contribuciones más prolíficas a la teoría de los determinantes fueron las del matemático francés Agustin-Louis Cauchy (1789-1857). Cauchy escribió, en 1812 una memoria de 84 páginas que contenía la primera demostración del teorema detAB=detA detB. En 1840 Cauchy hizo muchas otras contribuciones a las matemáticas. En su texto de cálculo de 1829 Leçons sur le calcul différential, dio la primera definición razonablemente clara de límite.

Cauchy escribió ampliamente tanto en las matemáticas puras como en las aplicadas. Solo Euler escribió más. Cauchy hizo contribuciones en varias áreas, incluyendo la teoría de las funciones reales y complejas, la teoría de la probabilidad, geometría, teoría de propagación de las ondas y las series infinitas.

A Cauchy se le reconoce el haber establecido nuevos niveles de rigor en las publicaciones matemáticas. Después de Cauchy, fue mucho más difícil publicar escritos basándose en la intuición; se exigió una estricta adhesión a las demostraciones rigurosas.

El volumen de las publicaciones de Cauchy fue abrumador . Cuando la Academis Francesa de Ciencias comenzó a publicar su revista Comptes Rendus en 1835, Cauchy envió su obra para que se publicara, en poco tiempo los gastos de impresión se hicieron tan grandes, solo por la obra de Cauchy, que la academia impuso un límite de cuatro cuartillas por cada documento a ser publicado.

Hay algunos otros matemáticos que merecen ser mencionados aquí. El desarrollo de un determinante por cofactores fue empleado por primera vez por el matemático francés Pierre de Laplace (1749-1827). Laplace es mejor conocido por la transformación que lleva su nombre que se estudia en los cursos de matemáticas aplicadas.

Un contribuyente principal de la teoría de los determinantes (estando solo Cauchy antes que él) fue el matemático alemán Carl Gustav Jacobi (1804-1851). Fue con él con quien la palabra “determinante” ganó la aceptación definitiva. Lo primero en lo que Jacobi empleó los determinantes fue en las funciones, al establecer la teoría de las funciones de varias variables. Sylvester llamó más tarde jacobiano a éste determinante.

Primeros cálculos de determinantes

En su sentido original, el determinante determina la unicidad de la solución de un sistema de ecuaciones lineales. Fue introducido para el caso de orden 2 por Cardano en 1545en su obra Ars Magna presentado como una regla para la resolución de sistemas de dos ecuaciones con dos incógnitas. Esta primera fórmula lleva el nombre de regula de modo.

El japonés  Seki introdujo los determinantes de orden 3 y 4 en la misma época que el alemán Leibniz.

La aparición de determinantes de órdenes superiores tardó aún más de cien años en llegar. Curiosamente el japonés Kowa Seki y el alemán Leibniz otorgaron los primeros ejemplos casi simultáneamente.

Leibniz estudió los distintos tipos de sistemas de ecuaciones lineales. Al no disponer de la notación matricial, representaba los coeficientes de las incógnitas con una pareja de índices: así pues escribía ij para representar a_{i, j}. En 1678 se interesó por un sistema de tres ecuaciones con tres incógnitas y obtuvo, para dicho ejemplo, la fórmula de desarrollo a lo largo de una columna. El mismo año, escribió un determinante de orden 4, correcto en todo salvo en el signo.¹ Leibniz no publicó este trabajo, que pareció quedar olvidado hasta que los resultados fueron redescubiertos de forma independiente cincuenta años más tarde.

En el mismo periodo, Kowa Seki publicó un manuscrito sobre los determinantes, donde se hallan fórmulas generales difíciles de interpretar. Parece que se dan fórmulas correctas para determinantes de tamaño 3 y 4, y de nuevo los signos mal para los determinantes de tamaño superior.² El descubrimiento se queda sin futuro a causa del cierre de Japón al mundo exterior por órdenes del shōgun, lo que se ve reflejado en la expulsión de los Jesuitas en 1638.